This is not intended to be a scientific paper, but a discussion of the disruptive light Chaos Theory can cast on climate change, for non-specialist readers. This will have a focus on the critical assumptions that global warming supporters have made that involve chaos, and their shortcomings. While much of the global warming case in temperature records and other areas has been chipped away, they can and do, still point to their computer models as proof of their assertions. This has been hard to fight, as the warmists can choose their own ground, and move it as they see fit. This discussion looks at the constraints on those models, and shows that from first principles in both chaos theory and the theory of modelling they cannot place reliance on these models.
First of all, what is Chaos? I use the term here in its mathematical sense. Just as in recent years Scientists have discovered extra states of matter (not just solid, liquid, gas, but also plasma) so also science has discovered new states that systems can have.
Systems of forces, equations, photons, or financial trading, can exist effectively in two states: one that is amenable to mathematics, where the future states of the systems can be easily predicted, and another where seemingly random behaviour occurs.
This second state is what we will call chaos. It can happen occasionally in many systems. For instance, if you are unfortunate enough to suffer a heart attack, the normally predictable firing of heart muscles goes into a chaotic state where the muscles fire seemingly randomly, from which only a shock will bring them back. If you’ve ever braked hard on a motorbike on an icy road you may have experienced a “tank slapper” a chaotic motion of the handlebars that almost always results in you falling off. There are circumstances at sea where wave patterns behave chaotically, resulting in unexplained huge waves.
Chaos theory is the study of Chaos, and a variety of analytical methods, measures and insights have been gathered together in the past 30 years.
Generally, chaos is an unusual occurrence, and where engineers have the tools they will attempt to “design it out”, i.e. to make it impossible.
There are, however, systems where chaos is not rare, but is the norm. One of these, you will have guessed, is the weather, but there are others, the financial markets for instance, and surprisingly nature. Investigations of the populations of predators and prey, for instance shows that these often behave chaotically over time. The author has been involved in work that shows that even single cellular organisms can display population chaos at high densities.
So, what does it mean to say that a system can behave seemingly randomly? Surely if a system starts to behave randomly the laws of cause and effect are broken?
A little over a hundred years ago scientists were confident that everything in the world would be amenable to analysis, that everything would be therefore predictable, given the tools and enough time. This cosy certainty was destroyed first by Heisenberg’s uncertainty principle, then by the work of Kurt Gödel, and finally by the work of Edward Lorenz, who first discovered Chaos, in, of course, weather simulations!
Chaotic systems are not entirely unpredictable, as something truly random would be. They exhibit diminishing predictability as they move forward in time, and this diminishment is caused by greater and greater computational requirements to calculate the next set of predictions. Computing requirements to make predictions of chaotic systems grow exponentially, and so in practice, with finite resources, prediction accuracy will drop off rapidly the further you try to predict into the future. Chaos doesn’t murder cause and effect; it just wounds it!
Now would be a good place for an example. Everyone owns a spread sheet program. The following is very easy to try for yourself.
The simplest man-made equation known that produces chaos is called the logistic map.
It’s simplest form is: Xn+1 = 4Xn(1-Xn)
Meaning that the next step of the sequence is equal to 4 times the previous step times 1 – the previous step. If we open a spread sheet we can create two columns of values:
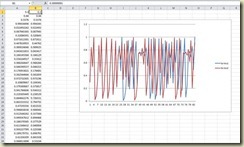
Each column A and B is created by writing =A1*4* (1-A1) into cell A2, and then copying it down for as many cells as you like, the same for B2, writing in =B1*4* (1-B1). A1 and B1 contain the initial conditions. A1 contains just 0.3 and B1 contains a very slightly different number: 0.30000001
The graph to the right shows the two copies of the series. Initially they are perfectly in sync, then they start to divert at around step 22, while by step 28 they are starting to behave entirely differently.
This effect occurs for a wide range of initial conditions. It is fun to get out your spread sheet program and experiment. The bigger the difference between the initial conditions the faster the sequences diverge.
The difference between the initial conditions is minute, but the two series diverge for all that. This illustrates one of the key things about chaos. This is the acute sensitivity to initial conditions.
If we look at this the other way round, suppose that you only had the series, and let’s assume to make it easy, that you know the form of the equation but not the initial conditions. If you try to make predictions from your model, any minute inaccuracies in your guess of the initial conditions will result in your prediction and the result diverging dramatically. This divergence grows exponentially, and one way of measuring this is called the Lyapunov exponent. This measures in bits per time step how rapidly these values diverge, averaged over a large set of samples. A positive Lyapunov exponent is considered to be proof of chaos. It also gives us a bound on the quality of predictions we can get if we try to model a chaotic system.
These basic characteristics apply to all chaotic systems.
Here’s something else to stimulate thought. The values of our simple chaos generator in the spread sheet vary between 0 and 1. If we subtract 0.5 from each, so we have positive and negative going values, and accumulate them we get this graph, stretched now to a thousand points.
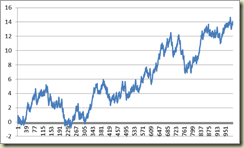
If, ignoring the scale, I told you this was the share price last year for some FTSE or NASDAQ stock, or yearly sea temperature you’d probably believe me. The point I’m trying to make is that chaos is entirely capable of driving a system itself and creating behaviour that looks like it’s driven by some external force. When a system drifts as in this example, it might be because of an external force, or just because of chaos.
So, how about the weather?
Edward Lorenz, (1917, 2008) was the father of the study of Chaos, and also a weather researcher. He created an early weather simulation using three coupled equations and was amazed to find that as he progressed the simulation in time the values in the simulation behaved unpredictably.
He then looked for evidence that real world weather behaved in this same unpredictable fashion, and found it, before working on discovering more about the nature of Chaos.
No climate researchers dispute his analysis that the weather is chaotic.
Edward Lorenz estimated that the global weather exhibited a Lyapunov exponent equivalent to one bit of information every 4 days. This is an average over time and the world’s surface. There are times and places where weather is much more chaotic, as anyone who lives in England can testify. What this means though, is that if you can predict tomorrows weather with an accuracy of 1 degree C, then your best prediction of the weather on average 5 days hence will be +/- 2 degrees, 9 days hence +/-4 degrees and 13 days hence +/- 8 degrees, so to all intents and purposes after 9-10 days your predictions will be useless. Of course, if you can predict tomorrow’s weather to +/- 0.1 degree, then the growth in errors is slowed, but since they grow exponentially, it won’t be many days till they become useless again.
Interestingly the performance of weather predictions made by organisations like the UK Met office drop off in exactly this fashion. This is proof of a positive Lyapunov exponent, and thus of the existence of chaos in weather, if any were still needed.
So that’s weather prediction, how about long term modelling?
Let’s look first at the scientific method. The principle ideas are that science develops by someone forming an hypothesis, testing this hypothesis by constructing an experiment, and modifying the hypothesis, proving or disproving it, by examining the results of the experiment.
A model, whether an equation or a computer model, is just a big hypothesis. Where you can’t modify the thing you are hypothesising over with an experiment, then you have to make predictions using your model and wait for the system to confirm or deny them.
A classic example is the development of our knowledge of the solar system. The first models had us at the centre, then the sun at the centre, then the discovery of elliptical orbits, and then enough observations to work out the exact nature of these orbits. Obviously, we could never hope to affect the movement of the planets, so experiments weren’t possible, but if our models were right, key things would happen at key times: eclipses, the transit of Venus, etc. Once models were sophisticated enough, errors between the model and reality could be used to predict new features. This is how the outer planets, Neptune and Pluto were discovered. If you want to know where the planets will be in ten years’ time to the second, there is software available online that will tell you exactly.
Climate scientists would love to be able to follow this way of working. The one problem is that, because the weather is chaotic, there is never any hope that they can match up their models and the real world.
They can never match up the model to shorter term events, like say six months away, because as we’ve seen, the weather six months away is completely and utterly unpredictable, except in very general terms.
This has terrible implications for their ability to model.
I want to throw another concept into this mix, drawn from my other speciality, the world of computer modelling through self-learning systems.
This is the field of artificial intelligence, where scientists attempt to create mostly computer programs that behave intelligently and are capable of learning. Like any area of study, this tends to throw up bits of general theory and one of these is to do with the nature of incremental learning.
Incremental learning is where a learning process tries to model something by starting out simple and adding complexity, testing the quality of the model as it goes.
Examples of this are neural networks, where the strength of connections between simulated brain cells are adapted as learning goes on or genetic programming, where bits of computer programs are modified and elaborated to improve the fit of the model.
From my example above of theories of the solar system, you can see that the scientific method itself is a form of incremental learning.
There is a graph that is universal in incremental learning. It shows the performance of an incremental learning algorithm, it doesn’t matter which, on two sets of data.
The idea is that these two sets of data must be drawn from the same source, but they are split randomly into two, the training set, used to train the model, and a test set used to test it every now and then. Usually the training set is bigger than the test set, but if there is plenty of data this doesn’t matter either. So as learning progresses the learning system uses the training data to modify itself, but not the test data, which is used to test the system, but is immediately forgotten by it.

As can be seen, the performance on the training set gets better and better as more complexity is added to the model, but the performance of the test set gets better, and then starts to get worse!
Just to make this clear, the test set is the only thing that matters. If we are to use the model to make predictions we are going to present new data to it, just like our test set data. The performance on the training set is irrelevant.
This is an example of a principle that has been talked about since William of Ockham first wrote “Entia non sunt multiplicanda praeter necessitatem “, known as Ockham’s razor and translatable as “entities should not be multiplied without necessity”, entities being in his case embellishments to a theory. The corollary of this is that the simplest theory that fits the facts is most likely to be correct.
There are proofs for the generality of this idea from Bayesian Statistics and Information Theory.
So, this means that our intrepid weather modellers are in trouble from both ends: if their theories are insufficiently complex to explain the weather their model will be worthless, if too complex then they will also be worthless. Who’d be a weather modeller?
Given that they can’t calibrate their models to the real world, how do weather modellers develop and evaluate their models?
As you would expect, weather models behave chaotically too. They exhibit the same sensitivity to initial conditions. The solution chosen for evaluation (developed by Lorenz) is to run thousands of examples each with slightly different initial conditions. These sets are called ensembles.
Each example explores a possible path for the weather, and by collecting the set, they generate a distribution of possible outcomes. For weather predictions they give you the biggest peak as their prediction. Interestingly, with this kind of model evaluation there is likely to be more than one answer, i.e. more than one peak, but they choose never to tell us the other possibilities. In statistics this methodology is called the Monte Carlo method.
For climate change they modify the model so as to simulate more CO2, more solar radiation or some other parameter of interest and then run another ensemble. Once again the results will be a series of distributions over time, not a single value, though the information that the modellers give us seems to leave out alternate solutions in favour of the peak value.
Models are generated by observing the earth, modelling land masses and air currents, tree cover, ice cover and so on. It’s a great intellectual achievement, but it’s still full of assumptions. As you’d expect the modellers are always looking to refine the model and add new pet features. In practice there is only one real model, as any changes in one are rapidly incorporated into the others.
The key areas of debate are the interactions of one feature with another. For instance the hypothesis that increased CO2 will result in run-away temperature rises is based on the idea that the melting of the permafrost in Siberia due to increased temperatures will release more CO2 and thus positive feedback will bake us all. Permafrost may well melt, or not, but the rate of melting and the CO2 released are not hard scientific facts but estimates. There are thousands of similar “best guesses’’ in the models.
As we’ve seen from looking at incremental learning systems too much complexity is as fatal as too little. No one has any idea where the current models lie on the graph above, because they can’t directly test the models.
However, dwarfing all this arguing about parameters is the fact that weather is chaotic.
We know of course that chaos is not the whole story. It’s warmer on average away from the equatorial regions during the summer than the winter. Monsoons and freezing of ice occur regularly every year, and so it’s tempting to see chaos as a bit like noise in other systems.
The argument used by climate change believers runs that we can treat chaos like noise, so chaos can be “averaged out”.
To digress a little, this idea of averaging out of errors/noise has a long history. If we take the example of measuring the height of Mount Everest before the days of GPS and Radar satellites, the method to calculate height was to start at Sea level with a theodolite and take measurements of local landmarks using their distance and their angle above the horizon to estimate their height. Then to move on to those sites and do the same thing with other landmarks, moving slowly inland. By the time surveyors got to the foothills of the Himalayas they were relying on many thousand previous measurements, all with measurement error included. In the event the surveyor’s estimate of the height of Everest was only a few hundred feet out!
This is because all those measurement errors tended to average out. If, however there had been a systemic error, like the theodolites all measuring 5 degrees up, then the errors would have been enormous. The key thing is that the errors were unrelated to the thing being measured.
There are lots of other examples of this in Electronics, Radio Astronomy and other fields.
You can understand climate modellers would hope for the same to be true of chaos. In fact, they claim this is true. Note however that the errors with the theodolites were nothing to do with the actual height of Everest, as noise in radio telescope amplifiers has nothing to do with the signals from distant stars. Chaos, however, is implicit in weather, so there is no reason why it should average out. It’s not part of the measurement; it’s part of the system being measured.
So can chaos be averaged out? If it can, then we would expect long term measurements of weather to exhibit no chaos. When a team of Italian researchers asked to use my Chaos analysis software last year to look at a time series of 500 years of averaged South Italian winter temperatures, the opportunity arose to test this. The picture below is this time series displayed in my Chaos Analysis program, ChaosKit.
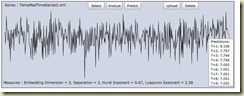
The result? Buckets of chaos. The Lyapunov exponent was measured at 2.28 bits per year.
To put that in English, the predictability of the temperature quarters every year further ahead you try to predict, or the other way round, the errors more than quadruple.
What does this mean? Chaos doesn’t average out. Weather is still chaotic at this scale over hundreds of years.
If we were, as climate modellers try to do, to run a moving average over the data, to hide the inconvenient spikes, we might find a slight bump to the right, as well as many bumps to the left. Would we be justified in saying that this bump to the right was proof of global warming? Absolutely not: It would be impossible to say if the bump was the result of chaos, and the drifts we’ve see it can create or some fundamental change, like increasing CO2.
So, to summarize, climate researchers have constructed models based on their understanding of the climate, current theories and a series of assumptions. They cannot test their models over the short term, as they acknowledge, because of the chaotic nature of the weather.
They hoped, though, to be able to calibrate, confirm or fix up their models by looking at very long term data, but we now know that’s chaotic too. They don’t, and cannot know, whether their models are too simple, too complex, or just right, because even if they were perfect, if weather is chaotic at this scale, they cannot hope to match up their models to the real world, the slightest errors in initial conditions would create entirely different outcomes.
All they can honestly say is this: “we’ve created models that we’ve done our best to match up to the real world, but we cannot prove to be correct. We appreciate that small errors in our models would create dramatically different predictions, and we cannot say if we have errors or not. In our models the relationships that we have publicized seem to hold.”
It is my view that governmental policymakers should not act on the basis of these models. The likelihood seems to be that they have as much similarity to the real world as The Sims, or Half-life.
On a final note, there is another school of weather prediction that holds that long term weather is largely determined by variations in solar output. Nothing here either confirms or denies that hypothesis, as long term sunspot records have shown that solar activity is chaotic too.
Andy Edmonds
06/06/2011
Short Bio
Dr Andrew Edmonds is an author of computer software and an academic. He designed various early artificial intelligence computer software packages and was arguably the author of the first commercial data mining system. He has been the CEO of an American public company and involved in several successful start-up businesses. His PhD thesis was concerned with time series prediction of chaotic series, and resulted in his product ChaosKit, the only standalone commercial product for analysing chaos in time series. He has published papers on Neural Networks, genetic programming of fuzzy logic systems, AI for financial trading, and contributed to papers in Biotech, Marketing and Climate.